Schaltregler sind ein effizientes Mittel, um Spannungen zu stabilisieren bzw. um aus einer Versorgungsspannung Betriebsspannungen unterschiedlicher Werte zu erhalten.
Die grundsätzliche Berechnung und Auslegung solcher Schaltregler ist mittlerweile kein Problem mehr, da die Datenblätter der entsprechenden Steuerbausteine hinreichend mit Formeln gespickt sind. Was hingegen schwerlich bis gar nicht zu finden ist, ist die Herleitung der einschlägigen Formeln. Daher soll an dieser Stelle der Versuch der mathematisch-technischen Beschreibung eines Abwärtswandlers "from scratch" unternommen werden.

Ein Abwärtswandler ("Buck-Regler") ist grundsätzlich folgendermaßen aufgebaut:

Die wesentlichen Komponenten sind (von links nach rechts):

1. Spannungsquelle V, liefert die Eingangsspannung U_IN

2. Schalter S, wird vom Regelkreis periodisch ein- und ausgeschaltet

3. Diode D

4. Spule L

5. Kondensator C

6. Regelkreis, überwacht die Ausgangsspannung und schaltet den Schalter entsprechend

Für die weitere Betrachtung teilen wir die Ausgangsspannung auf und definieren U_O als den konstanten Gleichspannungswert und ΔU(t) als den Wechselspannungsanteil, die sogenannte "Ripplespannung". In der Praxis wird bei Stromversorgungen letztere wesentlich kleiner sein als der Gleichspannungsanteil, daher soll er bei den folgenden Betrachtungen zunächst vernachlässigt werden - hierbei entfällt auch der Stromanteil i_C.

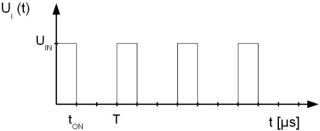
Da der Schalter periodisch ein- und ausgeschaltet wird, sieht die Spannung U_i(t) etwa so aus:

Während einer Periode T der Schaltfrequenz f ist der Schalter während der Zeitdauer t_ON geschlossen. Zwischen T und f gilt folgender Zusammenhang:

Während dieser Zeit fließt ein Strom durch die Spannungsquelle, den geschlossenen Schalter, die Spule und die Last am Ausgang; im Bild entlang der gestrichelten roten Linie:

Über der Spule liegt dann die Differenz der Spannungen U_IN und U_O an:

 Der Einfachheit halber soll angenommen werden, dass Ein- und Ausgangsspannung konstant bzw. die veränderlichen Anteile so klein sind, dass sie zunächst vernachlässigt werden können – das entspricht insofern der Praxis, als dass das Ziel ja eine konstante Ausgangsspannung mit kleinem Ripple-Anteil ist.

Für den Spulenstrom zum Zeitpunkt t gilt allgemein:

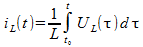
t₀ ist hier ein beliebiger Anfangszeitpunkt.
U_L(τ) ist die Spannung, die über der Spule liegt. Daher gilt mit Formel (2):  

U_IN und U_O sind, wie angenommen, in diesem Fall konstant und können vor das Integral gezogen werden. Damit ergibt sich:

  ... und mit gelöstem Integral:

=> Unter der Annahme, dass U_IN > U_O und der Schalter zwischen den Zeitpunkten t₁ und t₂ geschlossen ist, steigt der Spulenstrom ausgehend vom Anfangswert zum Zeitpunkt t=t₁ linear an.

Zum Zeitpunkt t=t_ON wird der Schalter S geöffnet. Jetzt befindet sich keine Spannungsquelle mehr im Stromkreis, allerdings wird in der Spule durch das zusammenbrechende Magnetfeld eine Spannung U_L(t) induziert, die den Stromfluß entlang der gestrichelten Linie durch den Pfad D - L - Last am Ausgang aufrecht erhält:

Eine ideale Diode vorausgesetzt, gilt jetzt 

Ganz wichtig zur Erinnerung: hier wird der Fall betrachtet, dass U_O weitgehend konstant bleibt. In Formel (3) oben zur Berechnung des Spulenstroms eingesetzt ergibt das:     

Der Strom fällt also ausgehend vom Wert beim Ausschalten des Schalters linear ab. Setzt man t=t_ON in Formel (5) ein:

 

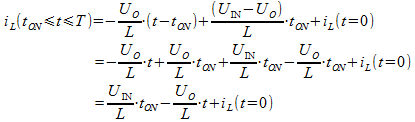
Der Spulenstrom sieht also so aus:

Es wurde hierbei zusätzlich zum „Startstrom“ i_L(t=0) noch der „Gleichstromanteil“ i_DC eingezeichnet; dieser liegt jeweils in der Mitte der steigenden bzw. fallenden Flanke des „Ripplestroms“.Aus den oben hergeleiteten Formeln lassen sich einige interessante (und vor allem aus Datenblättern bekannte) Erkenntnisse gewinnen.Geht man davon aus, dass quasi „statische“ Verhältnisse vorliegen und Ausgangsgleichspannung und -strom konstant sind, so muss der Spulenstrom am Ende der Periode, also zum Zeitpunkt t=T wieder den Anfangswert i_L(t=0) haben, also:

in Formel 8 eingesetzt ergibt sich folgender Zusammenhang:

Die Ausgangsspannung ist also direkt abhängig von der Eingangsspannung und dem Verhältnis von Einschaltzeitdauer zu Periodendauer; die Ströme und der Wert der Spule haben hierauf überhaupt keinen Einfluß!

Der Peak-to-Peak Wert des Ripplestroms der Spule i_LACpp ergibt sich dann aus dem Spitzenstrom zum Zeitpunkt t_ON abzüglich des Wertes zum Zeitpunkt t=0:

Formel (9) umgeformt ergibt:

Daraus folgt mit Formel (1)

Der maximal auftretende Spulenstrom ergibt sich dann aus dem Ausgangsgleichstrom plus der Hälfte des Ripplestromes:

Zu beachten ist, dass man bei der praktischen Dimensionierung der Spule für i_LDC mit dem Ausgangsstrom im Kurzschlußfall rechnen sollte.

Eine weitere Besonderheit rührt daher, dass der Spulenstrom aufgrund der Diode nicht die Richtung wechseln kann. Daraus kann man direkt folgern, dass der Ausgangsstrom i_DC (siehe Verlauf in der Grafik oben) nicht kleiner als der halbe Ripplestrom sein darf:

Ist das doch der Fall, dann wird die Ausgangsspannung unweigerlich steigen. Bei integrierten Schaltreglern wird in diesem Fall in der Regel der Betriebsmodus geändert und der Regler läuft im diskontinuierlichen Mode, d.h. die Schaltfrequenz wird kleiner.
→ Diesen Fall schaue ich mir an, wenn ich mal Zeit habe....! ;-)

Wenden wir uns den Verhältnissen am Ausgangskondensator zu. Zur Verdeutlichung nochmals der Aufbau der Schaltung mit allen auftretenden Spannungen und Strömen:

Für die Ströme am Ausgangsknoten gilt:

Unter Beibehaltung der oben bereits gemachten Annahme, dass die Ripplespannung wesentlich kleiner ist als der Gleichspannungsanteil, kann man schreiben:

Mit Formel (5) wird daraus:

Wie aus Abbildung 5 ersichtlich ist, ergibt sich i_L(t=0) aus dem Ausgangsgleichstrom abzüglich des halben Ripplestromes, also:

Mit

und Formel (10) folgt daraus:

Dieses Zwischenergebnis in Formel (16) eingesetzt ergibt:

Die gleiche Betrachtung soll für die Perioden mit geöffnetem Schalter erfolgen.
Wir erinnern uns – aus Formel (15):

Für den Zeitraum (t_ON ≤ t ≤ T) gilt laut Formel (8) für den Spulenstrom:

daraus folgt:

Mit i_L(t=0) aus Formel (17) ergibt dies:

Der Kondensatorstrom schaut demzufolge so aus:

Der zeitliche Verlauf des Stromes ist etwa dreieckförmig und wechselt die Richtung, je nachdem ob der Kondensator geladen oder entladen wird. Da ein Kondensator bekanntermaßen keinen Gleichstrom führen kann, pendelt der Strom um die Null-Linie herum.
Es stellt sich die Frage, warum der Kondensator zum Zeitpunkt t=0 bzw. in jedem Zyklus kurz nach dem Schließen des Schalters der Grafik nach ENTladen wird – dies wird aber klar, wenn man sich den Spulenstrom in Abbildung 5 anschaut: Dieser ist kurz nach dem Schließen des Schalters noch kleiner als der DC-Strom, der in die Last fließt. Also muss der benötigte Stromanteil dem Kondensator entnommen werden.

Der Spitzenstrom tritt u.a. auf zum Zeitpunkt t=t_ON. Mit Formel (19) ergibt sich dann:

dies führt umgeformt zu:

Ersetzt man t_ON mit dem Ergebnis von Formel (9), so wird daraus:

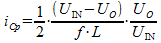
Aufgrund des dreieckförmigen Verlaufes des Kondensatorstroms beträgt dessen Effektivwert die Hälfte des Spitzenwertes, also:

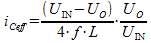
Aus dem zeitlichen Verlauf des Kondensatorstromes könnte man durch Integration der Formeln (18) und (19) auf die Ripplespannung schließen. Da aber die Rechnung zu Beginn der Überlegungen bereits dadurch entscheidend vereinfacht wurde, dass die Ausgangsspannung U_O (und damit die Spannung am Kondensator) als konstant angenommen wurde, wäre eine solche Berechnung wohl eher Zeitverschwendung. Darum soll zur Abschätzung ein anderer Ansatz verwendet werden.

Für die Ladung Q des Kondensators gilt:

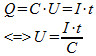
(22)Der Ausgangskondensator wird gemäß Abbildung 7 dann geladen, wenn der Graph im positiven Bereich ist. Dies ist der Fall im Bereich von

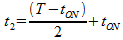
Die entsprechende Zeitdauer ist also:

Während dieser Zeit wird der Kondensator mit dem Effektivstrom aus Formel (21) aufgeladen. Damit folgt für die Spannung:

Interessant wird es in der Praxis jedoch, wenn in der „echten Welt“ beim „realen Kondensator“ ein leider ebenso realer ESR („Equivalent Series Resistance“) R_ESR ins Spiel kommt. Dieser trägt nämlich auch einen Teil zur Ripplespannung bei:

Dieser Anteil muss auf die Spannung U_Ceff vektoriell aufsummiert werden, da die beiden Spannungsanteile nicht gleichphasig, sondern um 90° phasenverschoben auftreten. Damit ergibt sich die vollständige Abschätzung des Effektivwertes der Ripplespannung zu: